
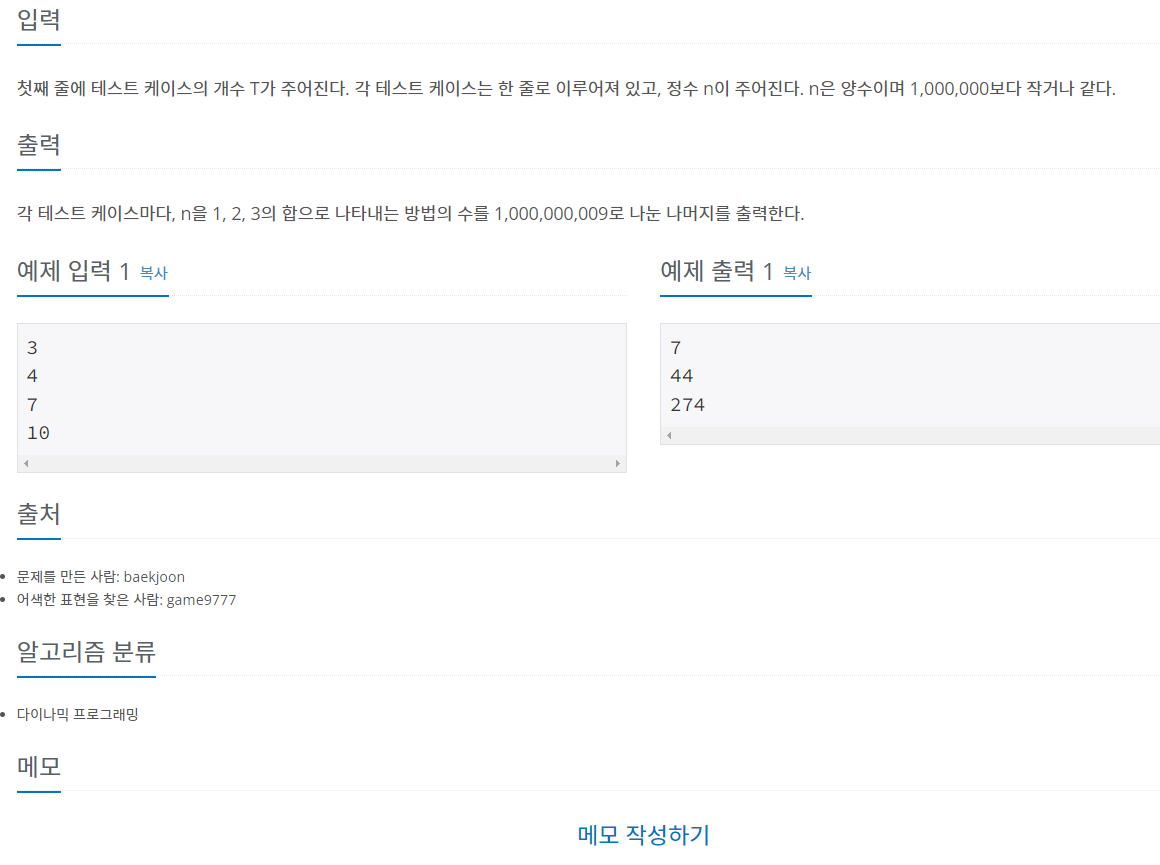
이런 문제에서, 초기에 제출한 코드의 경우

깔끔하게 틀려버렸다.
근데 논리는 문제가 없는것 같고, 뭔가 잘못되었을 곳으로 보여지는 부분이 int로 잡고 3개의 항을 더할때 int overflow가 발생할 수 있겠다 싶어서 d배열을 long long 으로 잡고 제출하니까

그대로 똑같은 논리로 전개하는 코드에서 정답을 얻을 수 있었다.
그래서 이 1'000'000만가지 경우까지 계산하는 코드를 1부터 1'000'000경우의 가지까지 출력을 했을때 변하는 값들을 확인해보니,

이런식으로 변해가는 상황이다.
이때 결국 d[i]는 1,000,000,009로 나눈 나머지 값들을 가져갈것이기 때문에 만약 d[i]의 값이 10억을 넘지 않는 선에서 크다면, 예를 들어 n=999995, n=999996 , n=999997번의 연속합을 이용해서 n=999998의 d[i]값을 구할때, 세 수의 합이 대략적으로 24억이니까 int로 설정시 %mod를 해주기 전에 int범위인 21억을 넘게 된다.
이렇게 int로 정의한 값이 결국 mod로 나누어서 21억의 범위를 넘지 않게 되더라도, 계산 과정 중간에 21억을 넘을때 어떻게 될지에 대해서 한번 코드를 작성해서 실행해보면,

적상적으로 동작하지 않게된다.
위 값의 경우는

이렇게 a+b+c를 d에 저장하고, 그리고 난 뒤에 d를 %mod 로 연산한 값과 동일하다
결국에는 결국 내가 원하는 계산값이 21억을 넘는 값을 마지막에 10억단위의 큰 값의 나머지를 구해서 마지막 결과는 21억을 넘지 않더라도, 계산 중간 과정상에서 int overflow가 발생하면서 프로그램이 정상적으로 동작하지 않게 되는것이다.
위와 같은 문제때문에 내가 처음에 작성한 코드의 경우, int 범위를 넘어가는 연산이 중간에 있는 풀이의 경우는 long long으로 선언해서 정답을 제출해서 풀어도 되고(내가 두번째로 시행한 방법)
애초에 int로 선언해서, 계산 과정상 문제가 될 부분이 없도록 만드는 풀이로 작성해도 된다.
그와 같은 풀이는
#include <bits/stdc++.h>
using namespace std;
int n;
int d[1000010];
int mod = 1e9 + 9;
int main(void){
ios::sync_with_stdio(0);
cin.tie(0);
d[1] = 1; d[2] = 2; d[3] = 4;
for(int i = 4; i <= 1000000; ++i)
for(int j = 1; j <= 3; ++j)
d[i] = (d[i] + d[i-j]) % mod;
int t;
cin >> t;
while(t--){
cin >> n;
cout << d[n] << '\n';
}
}이와같이 세 항을 다 더하면서 %mod를 해주기보다 각각의 항들을 더해서 %mod를 해주고, 그 값들을 더해서 %mod를 해주고, 그 값들을 더해서 %mod를 해주면서 결과적으로 마지막 d[i]의 값을 결정지어서 계산 과정상 int overflow가 일어나지 않도록 만들어줄 수 있다.
두가지 문제의 풀이방향중 어떤것을 선택하던지 상관은 없겠으나, 중요한것은 10억으로 나눈 나머지 라는 값을 구할때 결국 더해주는 항의 갯수, 더해주는 항의 값의 범위, 이런것들을 종합적으로 고려해서 계산 과정 중간에 int overflow가 발생할 수 있는지 없는지에 대해서 신중하게 판단하고 그 overflow 발생 가능성을 제거하는, 혹은 우회하는 코드를 작성해야 할것이다. 신중하게 작성하도록 하자.
'알고리즘 > BOJ' 카테고리의 다른 글
| 시간복잡도의 표현에 관하여. (0) | 2023.05.05 |
|---|---|
| c++ boj 1890번 문제를 통해서 알게된 간략하게 표현한 변수의 중요성. (0) | 2023.05.04 |
| stack과 같은 기능을 활용해야 하는데, 그 와중에 개별 원소에 접근해야 할때. 그럴땐 deque를 사용하자. (0) | 2023.05.03 |
| dp 문제에서 pre[] 배열을 선언해서 뒤로 추적해 나갈때 deque의 활용 (0) | 2023.05.02 |
| c++ 2차원 배열에서 *max_element를 사용하는 방법 (0) | 2023.05.02 |
