boj 7795번 문제를 통해. 접하게된 풀이 방법에 대하여.

boj 7795번 문제의 풀이를 내가 푼 방법과 다른 방법을 접하고, 그 방법에 대해서 이해하기 위해 기록을 남긴다. 

https://www.acmicpc.net/problem/7795

7795번: 먹을 것인가 먹힐 것인가

 

우선적으로 내 풀이는, 

#include <bits/stdc++.h>
using namespace std;

int arrA[20'005];
int arrB[20'005];

int main() {
	ios::sync_with_stdio(0); 
	cin.tie(0); 
	int t;
	cin >> t;
	while (t--) {
		int n, m;
		cin >> n >> m;
		int cnt = 0;
		for (int i = 0; i < n; i++)
			cin >> arrA[i];
		for (int i = 0; i < m; i++)
			cin >> arrB[i];
		sort(arrA, arrA + n);
		sort(arrB, arrB + m,greater<int>()); //greater로 하면 내림차순 정렬
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++) {
				if (arrA[i] > arrB[j]) {
					cnt += m - j;
					break;
				}
			}
		}//400'000'000(모두 계산해버리면 이정도)
		cout << cnt << '\n';
	}
}

2중 for 문을 이용하되 중간중간 연산 과정을 줄여서 시간복잡도를 줄여서 문제의 시간 제한을 통과하는 방법으로 해결하였다. 그리고 그 후에 접하게된 풀이 방법에 대해서 기록해보자면, 

// Authored by : BaaaaaaaaaaarkingDog
// Co-authored by : -
// http://boj.kr/c8698bc57ac343dea8f836660aecc0b4
#include <bits/stdc++.h>
using namespace std;

int main(void){
  ios::sync_with_stdio(0);
  cin.tie(0);
  int t;
  cin >> t;
  while(t--){
    int n, m;
    cin >> n >> m;
    vector<pair<int,int>> v(n+m);
    for(int i = 0; i < n; i++){
      int a;
      cin >> a;
      v[i] = {a, 0};
    }
    for(int i = n; i < n+m; i++){
      int b;
      cin >> b;
      v[i] = {b, 1};
    }
    sort(v.begin(), v.end());
    int cnt = 0; // 현재까지 나온 b의 개수
    int ans = 0;
    for(int i = 0; i < n+m; i++){
      if(v[i].second == 0) // 현재 보는 수가 A에 속한 수
        ans += cnt;
      else // 현재 보는 수가 B에 속한 수
        cnt++;
    }
    cout << ans << '\n';
  }
}

이렇게 A집합과 B 집합을 하나로 합쳐서 pair로 A집합의 원소인지 B집합의 원소인지 표시를 해준뒤에 sort를 진행해서 이 내부의 원소들의 정렬의 형태가 

 

{1,0}

{1,0}

        {1,1}

{3,0}

       {3,1}

       {6,1}

{7,0}

{8,0} 

의 형태로 정렬하는 것이고, 이때에 주어진 코드를 이용해서 이렇게 정렬된 vector 컨테이너 내의 원소들을 이용해서, 

 

{1,0}             ans+= 0 (cnt=0, ans=0)

{1,0}             ans+=0  (cnt=0, ans=0)

        {1,1}     cnt++     (cnt=1, ans=0)

{3,0}             ans+=1  (cnt=1, ans=1)

       {3,1}      cnt++     (cnt=2, ans=1)

       {6,1}      cnt++     (cnt=3, ans=1)

{7,0}             ans+=3  (cnt=3, ans=4)

{8,0}             ans+=3  (cnt=3, ans=7)

=>> ans==7

위와같은 형태로 좌측에 있는 원소에서 우측에 있는 원소들이 자신의 자리보다 다 위쪽에 있는것들을 더하고, 

우측에 있는 원소에 새롭게 도착하면 cnt++ 을 해주면서 그 후에 등장하게 될 좌측의 원소들에 더할 더 작은 원소들의 값을 증가시키는 과정을 n+m 회 거치면 문제에서 요구하는 값을 구할 수 있다. 

이때의 시간 복잡도에 대해서 찾아보면, 

 

첫번째, 내 풀이법의 경우, 

 

 

두번째, 접하게된 정답 코드의 경우, 

 

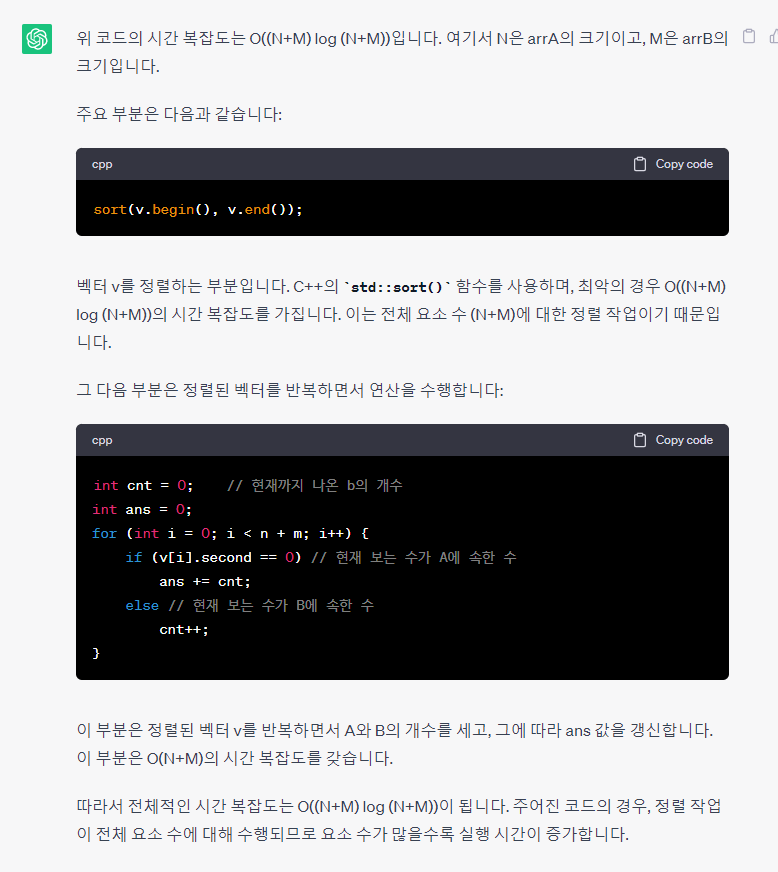
그리고 두 풀이법에 대한 시간복잡도의 비교에 대해서는, 

결국 이와같이 N과 M의 값이 어떤식으로 대소비교를 가지고 있느냐에 따라 다를것이다. 

접하게된 풀이 방법 또한 익혀서 다음에 이러한 문제를 만나게 되면 이러한 방법을 사용하여서 문제를 풀어보면서 이 방법에 익숙해져 보도록 하자. 

 

 

일단 내 풀이를 첫번째로 제출하였고, 그리고 새롭게 접하게된 풀이 방법을 통해서 제출했을때의 시간차이를 보면, 

이런식으로 큰 차이를 보인다. 물론 내 풀이도 충분하게 잘 통과한 것이지만, 이번에 접한 풀이법에 익숙해져서 더욱 효율적인 풀이를 할 수 있도록 노력해보자.